Multimagic series for cubes
See also the
multimagic series for squares
As we have seen for the smallest bimagic cube,
it may be interesting, in order to try to construct a p-multimagic cube of
order-n, to find all the p-multimagic series of order n, that is to say the
series of n different integers, from 1 to n3, having the correct magic, bimagic,...
to p-multimagic sums (= S1, S2,... Sp):
- S1 = n(n3 + 1)/2
- S2 = n(2n6 + 3n3 + 1)/6
- S3 = n(n9 + 2n6 + n3)/4 = n2 S12
- S4 = n(6n12 + 15n9 + 10n6 - 1)/30
- S5 = (3n2S22 - S3)/2
The order 3 allows one to get bimagic series.
Here are the 4 possible bimagic series:
- 3 19 20
- 4 15 23
- 5 13 24
- 8 9 25
So that means that:
- 3 + 19 + 20 = 4 + 15 + 23 = 5 + 13 + 24 = 8 + 9 + 25 = 42 = S1
- 3² + 19² + 20² = 4² + 15² + 23² = 5² + 13² + 24² = 8² + 9² + 25² = 770
= S2
For the order 4, there are 8 bimagic series for which the list is
given on the Smallest bimagic cube page.
Here is a summary of the number of multimagic series, some of these lists being downloadable as Excel files, from 44Kb to 540Kb each.
The numbers of bimagic series of orders 9 and 10 were computed by Walter Trump,
Germany, in October 2005. The number of trimagic series of order 9 was computed
by Gildas Guillemot, France, in December 2006 and later confirmed by
Michael Quist, USA, in May 2008. The numbers of bimagic series of orders
11 and 12 were computed in May and June 2013 by Walter Trump,
using a program written by Lee Morgenstern, USA. In August 2015, Dirk
Kinnaes, Belgium, confirmed the previously known numbers of bimagic
series, and computed the number of bimagic series of order 13: see his algorithm (PDF
file).
Number of multimagic series for cubes
|
Order
|
Bimagic
|
Trimagic
|
Tetramagic
|
Pentamagic
|
Hexamagic
|
|
3
|
4
|
0
|
0
|
0
|
0
|
|
4
|
8
|
0
|
0
|
0
|
0
|
|
5
|
272
|
0
|
0
|
0
|
0
|
|
6
|
25270
|
(a)
0
|
0
|
0
|
0
|
|
7
|
5152529
|
161
|
0
|
0
|
0
|
|
8
|
1594825624
|
17218
|
0
|
0
|
0
|
|
9
|
651151145259 |
363949
|
(b)
0
|
0
|
0
|
|
10
|
347171191981324 |
(a)
0
|
0
|
0
|
0
|
|
11
|
315035719463520007
|
Unknown! (d) (f) > 5.4 · 109
|
(e) 0
|
0
|
0
|
|
12
|
333498789992790704850
|
Unknown! (d) (f) > 2.5 · 1012
|
(e) 0
|
0
|
0
|
|
13
|
450285458654002877929960
|
Unknown! (d) (f) > 1.6 · 1015
|
Unknown! (d)
|
(e) 0
|
0
|
|
14
|
Unknown! (c) ~ 7.4 · 1026
|
(a)
0
|
0
|
0
|
0
|
|
15
|
Unknown! (c) ~ 1.5 · 1030
|
Unknown! (d) (f) > 1.4 · 1021
|
Unknown!!!!!!
|
(e) 0
|
0
|
|
16
|
Unknown! (c) ~ 3.7 · 1033
|
Unknown! (d) (f) > 1.9 · 1024
|
Unknown! (d)
|
Unknown! (d)
|
(e) 0
|
|
17
|
Unknown! (c) ~ 1.1 · 1037
|
Unknown! (d) (f) > 3.0 · 1027
|
(e) 0
|
0
|
0
|
|
18
|
Unknown! (c) ~ 3.7 · 1040
|
(a)
0
|
0
|
0
|
0
|
(a) Trimagic series of order 4k+2 are impossible: it is
impossible to have S3 even, with S1 odd and S2 odd.
(b) Short and
nice proof by Robert Gerbicz, Hungary, in January 2006. "For the order 9, the tetramagic sum is S4=510,118,152,189==13 mod 16.
But (2*x+1)^4==1 mod 16 and (2*x)^4==0 mod 16: it means that at least
13 odd numbers are needed. Impossible with only 9 numbers!"
(c) Estimations of bimagic series by Michael Quist,
June 2013.
(d) Unknown numbers of series, but existing series, examples
found by Lee Morgenstern, April-May 2015
(e) Impossibility
proofs by Lee Morgenstern, April-May 2015
(f) Estimations of trimagic series by Dirk
Kinnaes,
March 2017
In June 2013, Michael Quist wrote a paper estimating the
numbers of magic and multimagic
series,
including bimagic series for cubes of order N. See http://arxiv.org/abs/1306.0616.
Here is his formula, and the
obtained numeric values for 10 ≤ N ≤ 18. The error decreases with
higher orders. In August 2015, Dirk Kinnaes improved Quist's formula,
adding a new term (see also his PDF file given above).
Estimated numbers of bimagic series, formula by Michael
Quist:
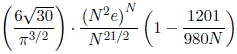
Improved
adding + 16333813 / 7847840N² term, by Dirk Kinnaes.
Comparison with the true numbers.
Order | Quist
estimated number | Kinnaes
estimated number | True number | Quist
error | Kinnaes
error |
10 | 3.607 · 1014 | 3.693 · 1014 | 347171191981324 | +3.90% | +6.36% |
11 | 2.971 · 1017 |
3.029 · 1017 |
315035719463520007
| -5.68% | -3.86% |
12 | 3.197 · 1020 |
3.248 · 1020 |
333498789992790704850
| -4.15% | -2.61% |
13 | 4.365 · 1023 | 4.424 · 1023 |
450285458654002877929960
| -3.07% | -1.75% |
14 | 7.389 · 1026 | 7.475 · 1026 | ? | ? |
?
|
15 | 1.521 · 1030 | 1.536 · 1030 | ? | ? |
?
|
16 | 3.747 · 1033 | 3.780 · 1033 | ? | ? |
?
|
17 | 1.089 · 1037 | 1.098 · 1037 | ? | ? |
?
|
18 | 3.691 · 1040 | 3.716 · 1040 | ? | ? |
?
|
In March 2017, Dirk Kinnaes wrote a paper
"Estimating the number of K-multimagic hypercube series" (PDF
file) including a formula estimating the numbers of trimagic series
for cubes of order N. Here is his formula, and the obtained numeric values for
7 ≤ N ≤ 15. The error will decrease with
higher orders, we should expect much smaller errors for orders > 10.
Estimated numbers of trimagic series,
formula by Dirk
Kinnaes:
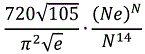
Comparison with the true numbers.
Order | Kinnaes
estimated number | True number | Kinnaes
error |
7 | 7.0 | 161 | / 23.1 |
8 |
544.0 |
17218
| / 31.6 |
9 |
74781.2 |
363949
| / 4.9 |
10 | 1.65 · 107 |
0
| --- |
11 | 5.42 · 109 | ? |
?
|
12 | 2.52 · 1012 | ? |
?
|
13 | 1.60 · 1015 | ? |
?
|
14 | 1.33 · 1018 | 0 |
---
|
15 | 1.41 · 1021 | ? |
?
|
The bimagic and trimagic series are referenced respectively under the
numbers A090653 and A092312
in the On-Line Encyclopedia of Integer Sequences, OEIS
Foundation.
Return to the home page http://www.multimagie.com