The Center Cell of a Magic 5³ is 63.
Original proof that the center of a perfect magic of order 5 is 63, by Richard Schroeppel, 1976.

The coordinates of the cells in the cube are 0, 1, 2, 3, or 4. The center of the cube is (2,2,2). G is the group of permutations of the cells of the cube which preserve linehood, g is in G iff for all lines L in the cube, gL is also a line.

Lemma:    G has 192 elements, and is generated by the elements g1, g2, g3, g4, and g5, which map the cell (i,j,k) into (j,i,k); (j,k,i); (4-i,j,k); s(i,j,k); and t(i,j,k). s(0,1,2,3,4)=(1,0,2,4,3) and t(0,1,2,3,4)=(4,1,2,3,0).

Proof:    Ommited. Tedious.

There are six distinct classes of cells under G, and seven classes of lines. (Two cells are in the same class iff there is an element of G which maps one cell to the other.) All classes except B and C may be distinguished by the number of lines going through a cell. B and C are distinct because C lies on a line through the center cell, and B does not.

Cell class	Example	Number of cells in class	Number of lines through cell
A	(0,0,0)	16	7
B	(0,0,1)	48	4
C	(0,0,2)	24	4
D	(0,1,2)	24	3
E	(0,2,2)	12	5
F	(2,2,2)	1	13

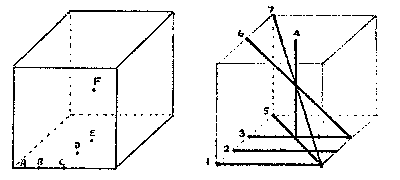(Original image as drowned by R. Schroeppel)

Line class	Endpoints of example	Number of lines in class	Average equation (see below)
1	(0,0,0)-(0,0,4)	24	2a + 2b + c = K
2	(0,1,0)-(0,1,4)	24	4b + d = K
3	(0,2,0)-(0,2,4)	24	2c + 2d + e = K
4	(2,2,0)-(2,2,4)	3	4e + f = K
5	(0,0,0)-(0,4,4)	24	2a + 2b + e = K
6	(2,0,0)-(2,4,4)	6	4c + f = K
7	(0,0,0)-(4,4,4)	4	4a + f = K

Suppose we have a particular magic 5³. K is the constant of the cube, 315. Let a, b, c, d, e, and f be the averages of the entries in each class of cells. Select one line from each class of line. Each line can be interpreted as an equation between the five cells of the line and K. Map the line under G, obtaining 192 equations. Average the equations. Each element in the original equation is now replaced with its class average. Thus, we obtain the seven equations in the above table.

We conclude from equations 7, 6, and 4 that a = c = e. From equations 3 and 5 we get that b = d. Now equation 2 gives b = d = K/5. Equation 1 gives a = K/5, and equation 7 gives f = K/5. Therefore, each cell class has average value K/5. In particular, class F, which contains only the center cell (2,2,2), has average value K/5 = 63.

Richard Schroeppel
Santa Monica, California
November 16, 1976

Return to the home page http://www.multimagie.com